If we apply the concept of Parmenides of Elea on the universe we are actually modelling the structure of the volume of the universe. Not with the help of all the detailed descriptions of the observable and detectable phenomena, but with the properties of the dynamical volume of the universe. A model that envelopes the corresponding descriptions of the basic quantum fields.
If we try to better understand physical reality – actually constructing better models – it is common to focus on specific phenomena to get results. But there are ten thousands of papers that describe different aspects of specific phenomena. Not only in relation to the outcome and interpretation of experiments but also in relation to theoretical “exercises” to analyse (speculative) hypotheses in relation to different conceptual and mathematical approaches.
However, are the properties of specific phenomena under different conditions really useful for this type of research? Is it not reasonable to focus on properties that exist everywhere in the universe, no matter if it is part of a phenomenon or part of vacuum space? In other words, universal properties like the properties of the basic quantum fields because it is thought that these fields tessellate the volume of our universe.
Figure 1 shows in a schematic way the concept of Parmenides of Elea (≈ 500 B.C) about the reality that underlies our universe. A non-observable reality that is responsible for the emerging of relational reality. Like the underwater part of an iceberg is responsible for the part that is drifting above the waves. Parmenides argued that “nothing” cannot exist in our universe so he stated that the underlying creating reality exist also in empty space between the stars.
The paradox of Achilles and the tortoise, described by Zeno of Elea, shows that Parmenides’ underlying reality has a metric (see the paradoxes of Zeno in Wikipedia). That is obvious because Parmenides was a famous mathematician and an all-inclusive volume without a structure has no meaning in geometrical models of the universe. Moreover, Parmenides argued that there exist no real motion in our universe, motion is an illusion. In line with the results of all the experiments in physics that show that observable reality is strictly relational.
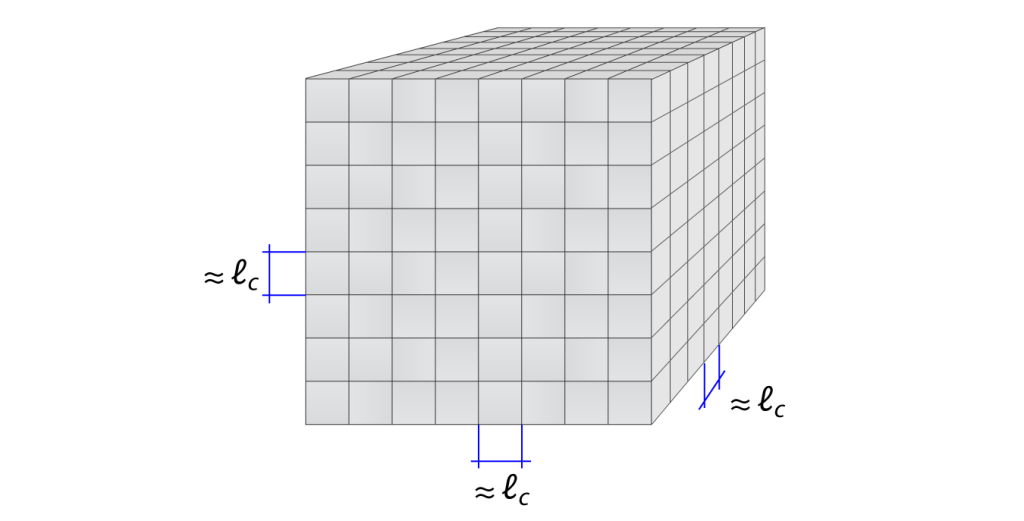
figure 1
The large cube in figure 1 represents the universe and the small cubes show Parmenides’ metric. Change is only possible if the units – the small cubes – have not only invariant properties but also variable properties.
It is obvious that a metric is only possible if the amount of volume of every unit is identical and invariant. That means that change is still possible if the surface area of every unit is variable. In other words, the small cubes are topological objects that deform their shape continuously under invariant volume (topological homeomorphism).
The image shows that an invariant volume cannot be deformed into a nearly 2D object (a sheet) because all the units have identical invariant and variable properties. But it also shows that one unit cannot deform its shape independently from all the other units around. All the units of the structure of the universe have to deform synchronously under influence of the invariant volumes.
Suppose the structure of our universe is static, like the large cube in figure 1. It immediately raises the question what determines the shape of each unit. I don’t mean the mutual influence of a unit in relation to its adjacent units, it is about the mechanism that is responsible for the shape of its internal (invariant) volume. This mechanism must show itself in relational reality. In other words, if every unit has an internal cubical shape forming mechanism the dominant shape in our universe will be the cube. So it is reasonable to conclude that there must be a direct relation between the internal shape forming mechanism of every unit and the dominant shape in our universe: the sphere.
Unfortunately, we cannot fill the volume of our universe with identical spheres because packed spheres don’t share their surface area. Packed spheres have only points of contact. The only solution is to imagine that all the units of the structure of the universe are deformed spheres. That means that a part of the volume of the unit has the configuration of a sphere (the inscribed sphere) and the left over part is deformed under influence of the adjacent units (the topological homeomorphism).
Now we have divided the volume of the universe into 2 parts: an amount of volume (≈ 74%) that is occupied by a lattice of spheres and an amount of volume (≈ 26%) that represents the deformed parts of each unit. The first volume (≈ 74%) must be a universal scalar field (the Higgs field) and the second volume (≈ 26%) is a universal topological field (the electric field).
If all the units deform in a synchronised way under influence of the identical spherical shape forming mechanism of each unit, the continuous deformation is quantised. Because 1 unit cannot interrupt the synchronised deformation of all the other units. The deformation has a duration thus the linear propagation of 1 fixed amount of topological deformation (h) in vacuum space has a fixed velocity (c).
Conclusion
Parmenides’ concept of an underlying creating reality explains the existence of the 2 universal conservation laws (energy and momentum), the 2 universal constants (h and c), the mechanism behind change/motion (the spherical shape forming mechanism) and the principle of non-locality. An indication that Parmenides’ model is trustworthy. More details can be find at Zenodo.org or in the references[1][2][3]
References:
- (2019); “Empiricism and empirical information”
https://zenodo.org/record/3592378 - (2025); “On the geometrical structure of quantised space”
https://zenodo.org/record/14556269 - (2020); “On the construction of the properties of discrete space”
https://zenodo.org/record/3909268