Humans have the awareness of the existence of a not linear time. An awareness that seems to contradict the existence of the constant of quantum time (1 tq). It seems to defy cause and effect too and give raise to the experience that humans have some kind of free will. The feeling that an amount of “will power” can change the phenomenological world that surrounds us. Actually changing relational reality.
In vacuum space the deformation of a unit of quantised space is limited to the spots around the points of contact of the scalar of the unit and the scalars of the adjacent units around. Figure 1 shows the topological deformation between 2 units (left side). Drawn is the cross section, the face of the right unit and at the right hand a larger cross section (ris = 1.0 is the radius of every scalar where the Higgs field is flat).
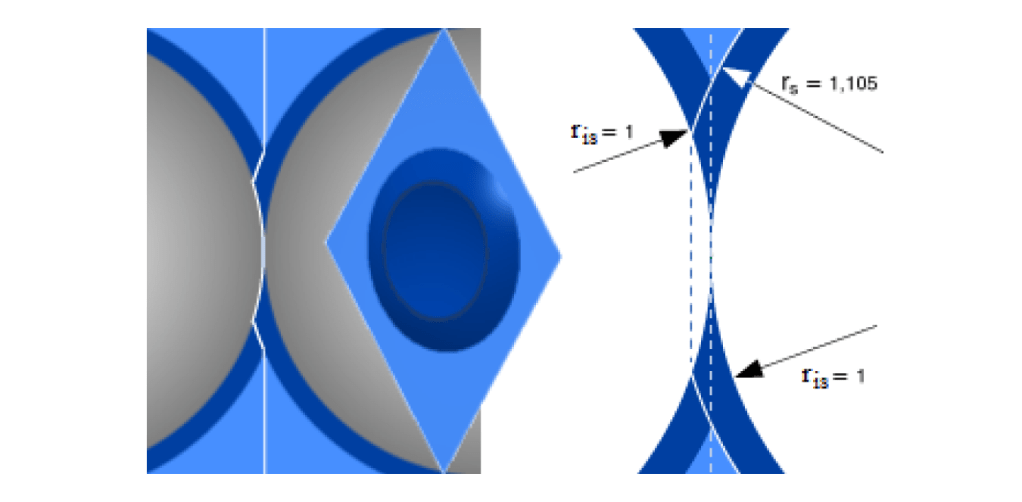
figure 1
The “nature” of the scalar can be described as the not deformed part of the scalar mechanism of the unit (I). So its resistance against the deformation by the scalar mechanism of the other units around is active in the points of contact with the adjacent scalars. It can be described with the help of vectors (II). However, the scalar mechanism itself is a spherical shape forming mechanism so the scalar represents also the concept of a sphere that is build up by infinite small concentric shells (III), a bit comparable with the layers of an onion. Figure 2 shows the 3 descriptions.
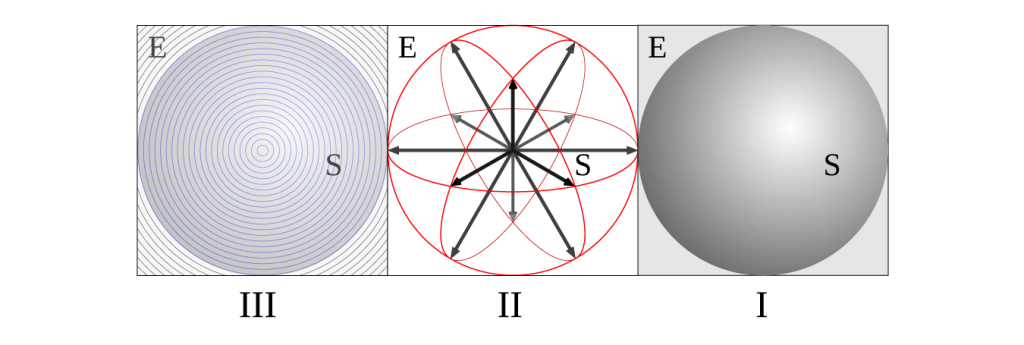
figure 2
If we imagine the decrease of a scalar under influence of the “push” by a large amount of involved units – for example the scalar in figure 2, image II – the question arises how much surface area of the unit is involved. Theoretically, every unit cannot transfer more topological deformation than ½ the quantum of energy during the constant of quantum time (1 tq). Although it is hard to imagine what is exactly going on because of the different “velocity” between the quantum of energy (c) and a vector (> c).
Figure 3 shows in a schematic way a rest mass carrying particle (black) with a decreased scalar inside (red). Because of the decreased scalar the adjacent scalars and all the other scalars around the adjacent scalars get vectorised. Simply because the 12 points of contact of each of the 12 adjacent scalars are reduced to 11 points of contact, creating an asymmetrical distribution of the not deformed scalar mechanism of these units. Just imagine that in figure 2, image II one vector disappears. It is obvious that this will create an unbalance inside the scalar under influence of all the other scalars “behind”.
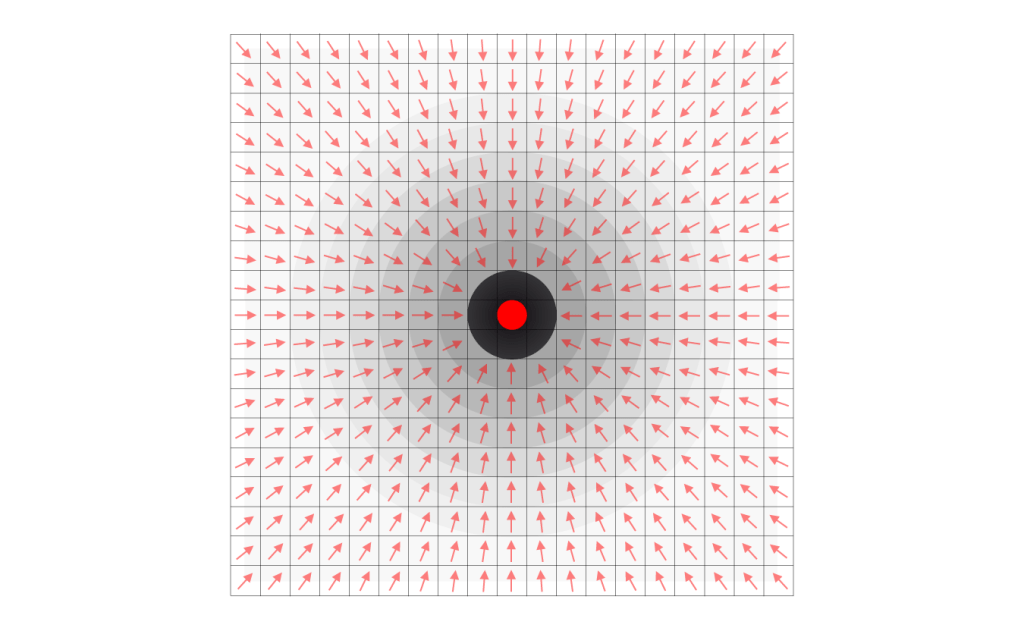
figure 3
The unbalance creates resulting vectors in vacuum space around (red arrows) and these vectors determine the topological deformation of the deformed part of the units around (rasterised concentric shells). The increasing topological deformation towards the particle is equal to the local energy density of the universal electric field (QFT). The vectors in figure 3 are resulting vectors, because the red arrows represent more than 1 vector of the unit. Like the real shape of the units is not cubic either.
Every unit transforms its shape with the same amount of topological deformation if we express the deformation with the help of the transferred internal volume to acquire the next shape. In between there is deformation too but we can only measure the change of the direction of the topological deformation (the cause behind the existence of the Planck constant). Because of the synchronisation of the changes of the shape of every unit of quantised space a measurement instrument (and our senses) cannot “signal” the transfer of the flux of infinite small volume inside every unit. That is why for measurement instruments and for humans phenomenal reality is limited to energy configurations.
The consequence is that during 1 tq (constant of quantum time) all the involved units in figure 3 transform in such a way that the observer thinks that the particle have moved a little bit in relation to the rest frame of quantised space (the schematic cubic grid). Of course, the observer doesn’t see that the whole volume – the particle and the topological deformation of all the other involved units around – has moved as a whole. The consequence is that the velocity of the rest mass is determined by the amount of quanta that has to be transferred to “move” the particle and everything around from 1 unit to an adjacent unit.
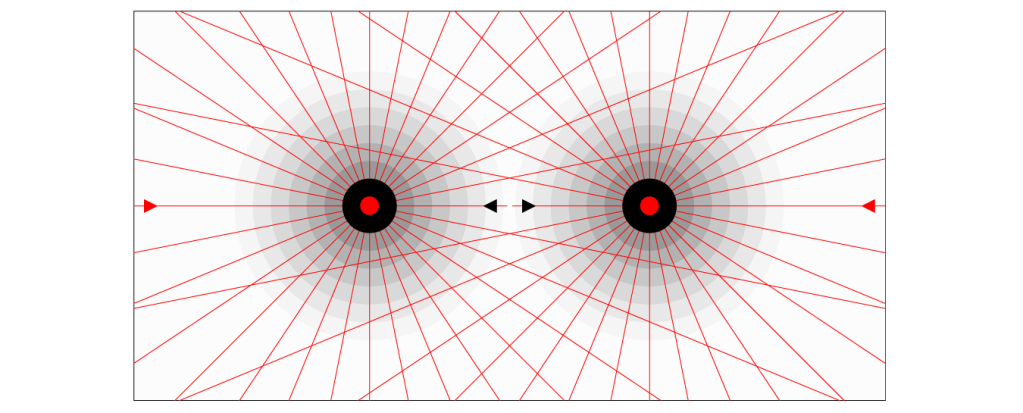
figure 4
The image in figure 3 shows just 1 rest mass carrying particle. If I draw 2 particles – see figure 4 – the local conditions are quite different. Because the symmetrical distribution of vectors around each particle is disturbed by the other particle (decreased scalars cannot mediate vectors). The effect on both particles is a push from vacuum space around (red) that influences the direction of the propagation of both particles in relation to the rest frame. However, the vectorisation (red arrows in figure 3) originate from the decreased scalar. The consequence is that the sum of the magnitude of the vectors of each particle is a bit comparable with a constant. Although the average properties of vacuum space around influence the size of the volume that can be thought as “vectorised space” (the red arrows that point towards each particle).
However the sum of the magnitudes of all the vectors in the universe is conserved, like all the energy changes in the universe are conserved. In other words, figure 4 shows that the existence of matter at every scale size results in the existence of “displaced vectors” (see previous post).
Conclusion
The emergence of matter in the universe started the creation of relative independent configurations of local displaced vectors. It doesn’t mean that the correspondence between the universal electric field and the magnetic field was lost. It changed the symmetry between the universal electric field and its corresponding magnetic field into an asymmetrical correspondence. The emergence of another type of interference between both fields that is termed “live” in our scientific culture.